Origami: What One Can Get via Paper Folding (Rus)
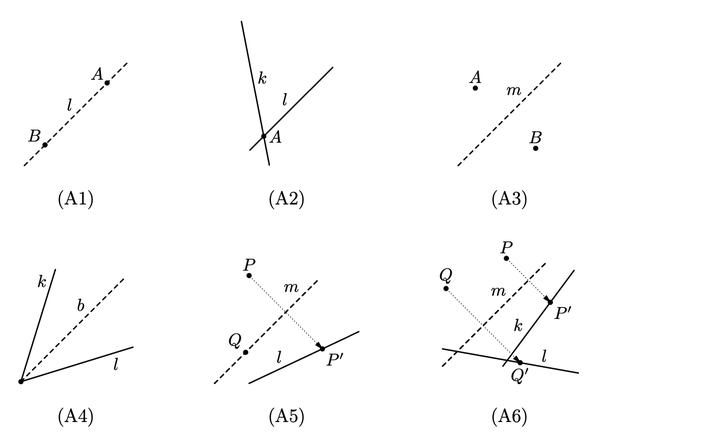 origami axioms
origami axioms
Abstract
In this work we study the set of origami numbers, more precisely the set of coordinates of points that could be reached via paper folding. In the scope of this work we show that this set is a square and cubic roots extension of $\mathbb{Q}$. It shows that using paper folds it is possible to get all the points that are reachable by ruler-and-compass construction and even more, for example angle trisection and doubling the cube.
Type